国家发展改革委等部门关于印发《电解铝行业节能降碳专项行动计划》的
科学计算在环境科学中的应用
科学计算在环境科学中的应用环境修复网讯:1 科学计算简介科学计算即数值计算,是指利用计算机完成科研和工程中复杂的数学计算,再现、预测和发现客观世界运动规律和演化特征的过程。科学计
环境修复网讯:1 科学计算简介
科学计算即数值计算,是指利用计算机完成科研和工程中复杂的数学计算,再现、预测和发现客观世界运动规律和演化特征的过程。
科学计算过程主要包括:建立数学模型、建立求解方法和计算机实现(部分依靠编程)三个步骤。
2 科学计算在环境科学中的重要地位
环境科学的研究对象是环境系统本身,而环境系统是环境各要素及其相互关系的总和,是一个复杂的多元动态开放系统,具有时间、空间、数量和质量等多个变量。随着研究的深入,人们逐渐意识到,对于环境系统的研究需要量化,分割研究,然后简单加和的形而上学的研究方法并不适合复杂的环境系统。由此,大量科研工作人员置身于环境系统理论研究,希望通过以数学模型来模拟环境系统,预测环境系统的变化规律。虽然,这些数学模型被人们广泛认可,但是模型求解困难成为实际应用的瓶颈。
随着科学技术发展,计算机水平不断进步,科学计算逐渐被应用于环境科学。大量基于科学计算的计算机语言和软件的出现,有效解决了环境系统模拟存在的计算问题,为环境系统的量化认识、优化规划、准确调控以及科学决策奠定基础。
如今,在环境科学研究、工程实践、环境规划、环境评价以及环境管理等工作中,科学计算发挥着越来越重要的作用。科学计算在环境科学中的应用总结如图所示:
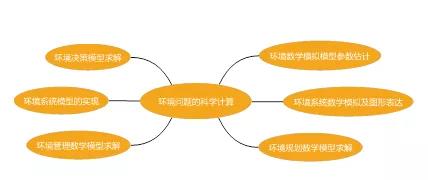
图1 科学计算在环境科学的应用
3 科学计算在环境科学中应用实例分析
为进一步理解科学计算在环境科学中的应用,下面以实际的例子进行分析。
例:现有一连续排污的污染点源向河流中排污,污染物的初始浓度为0.04mg/m3,河流流速为1.2m/s,污染物在河水中的扩散系数为15m2/s,求该污染物在河流中的时空分布和500米处污染物浓度达到稳态的时间。
求解过程如下:
采用有水流稳态源时间扩散模型
已知:有水流稳态源时间扩散模型描述的是连续稳定污染点源在形成稳态浓度前,各个空间点上的浓度随时间变化和模拟污染物在水流中形成稳态浓度后的情况。该模型为:
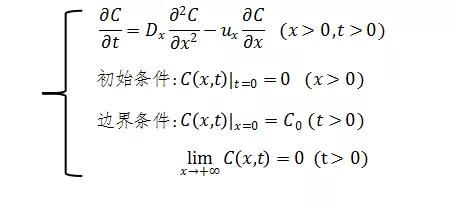
偏微分方程的解析解为:
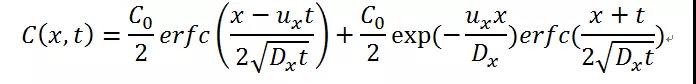
其中,erfc为余误差函数:
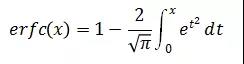
对于该模型,显然,很难通过人工计算进行求解。这里采用Matlab语言对上述问题进行分析,结果如图所示:
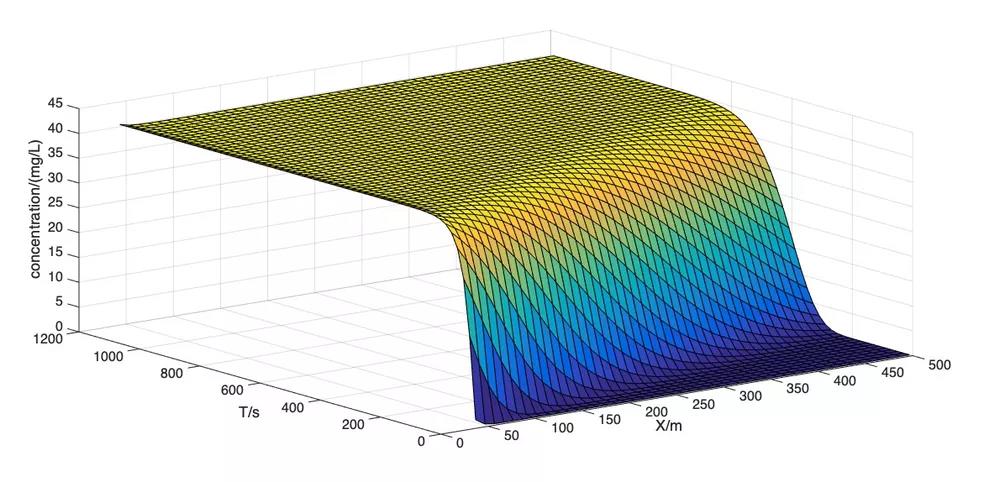
(a)浓度随时空变化
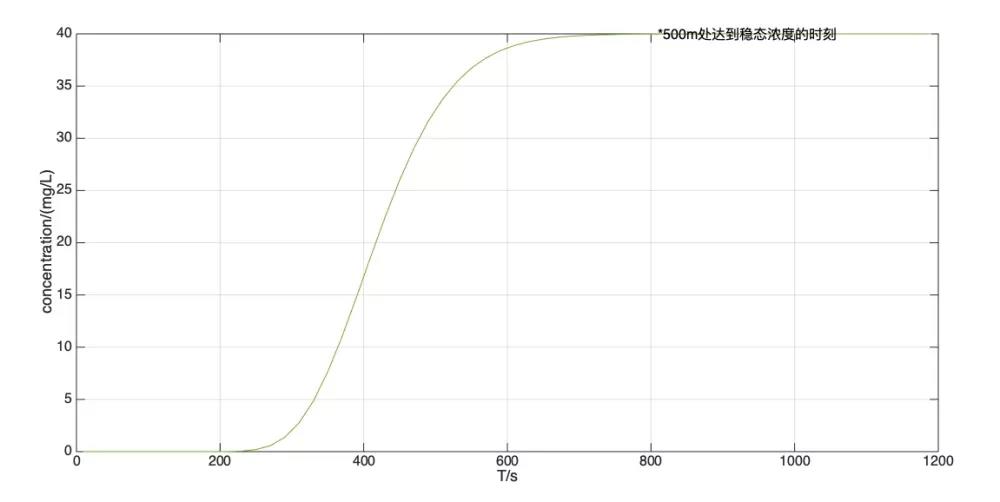
(b)500米处浓度变化过程
图2 Matlab求解结果
由图可知,不同距离处的污染物达到稳定浓度(40mg/L)所需时间不一样,同时,500米处的浓度由0逐渐上升,在803秒时达到稳定。
实际应用中,科学计算可以对实验数据、调查数据、工程数据进行统计、拟合、回归等数学处理分析,也能够求解一些复杂模型,预测环境系统变化趋势,从大量杂乱无章的数据中发现科学规律。定量化和模型化逐渐成为环境科学的一种发展趋势,而科学计算在其中扮演着举足轻重的作用。
原标题:科学计算在环境科学中的应用
-
海南国美采取多项安全购物环境措施全面实施疫情防控工作2024-08-19
-
⚠️抗击疫情,科学防疫2024-08-19
-
【科学防护】工作场所新型冠状病毒感染肺炎预防手册2024-08-19
-
生态环境部:确保疫情防控期间环境质量安全 防止疫情次生灾害2024-08-19
-
全球看武汉|香港反思SARS:高密度城市如何提升通风环境2024-08-19
-
肺炎疫情医疗废物应急处置如何做?生态环境部这样要求2024-08-19
-
严防严控 科学应对 全力打赢疫情防控阻击战 我市召开应对疫情工作协调会议 张瑞书主持会议并讲话2024-08-19
-
环境部:疫情防治产生的感染性医疗废物实行分类分流管理2024-08-19
-
生态环境部:将疫情防治过程中产生的感染性医疗废物实行分类分流管理2024-08-19
-
上海召开疫情防控专家座谈会,专家:本市防控措施科学、高效2024-08-19
-
出版界紧急上线一批数字读物,普及疫情防控科学知识2024-08-19
-
新型肺炎科学隔离指南2024-08-19
-
如何有效防控疫情?不妨善用行为科学2024-08-19
-
我市各部门各县区科学有效有序落实疫情防控措施2024-08-19
-
科学防治精准施策 坚决打赢疫情防控阻击战2024-08-19


