超声波气体流量计检测精度影响因素分

环境监测网讯:摘要：随着国家煤改气工程的推进，对天然气管道运输及测量技术的要求也越来越高。超声波流量计因测量稳定、压力损失小以及安装简便等特点使其在石油化工、冶金、电力等工程领域的应用越来越广泛。在当今多种超声波流量计中，时差法超声波流量计是应用最为广泛的，其检测原理是计算声道传播路径上的平均速度，并通过修正系数补偿的方式来得出管道的截面速度。然而，超声波流量计的测量精确度会受到诸多因素的影响，如输送流体的性质、管道内流体雷诺数、流量计的安装位置和声道位置等，这些参数的变化都会对超声波流量计测量时间差造成影响。

1导言

随着天然气运输贸易的发展，天然气需求量将越来越高。当前运输天然气最常见的方式就是通过管道运输，因此对天然气输送量的精确监测对于预防管道泄漏等安全事故有着重要意义。而从当前研究文献来看，关于超声波流量计在天然气流量监测测量中的精度影响因素报道比较少见。天然气由于密度、黏度均低于空气，因此在相同实验条件下其管道内流体速度分布也会有很大区别。

2检测原理

2.1超声波流量计测量原理

通过流量计上、下游探头来测量超声波在气体管道的顺流、逆流响应时间，得出体积流率的计算公式如下：

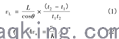
式中，vm———管道截面速度

vL———声道上流体平均线速度

L———流量计探头之间的声道长度

t1和t2———分别表示管道内流体顺流、逆流的传播时间

θ———声道与管道轴线的夹角

Q———管道内流体的体积流量

A———管道的横截面积

K———修正系数

2.2管道内气体速度分布

由于气体的黏度作用，管道截面处流体速度呈梯度分布，管道中心轴线处流速最高，贴近管道壁面处流速为0，当管道内任意位置截面处气体速度分布情况相同，则认为气体流动达到充分发展。根据雷诺数大小可以将流体流动状态分为2种，即层流状态和湍流状态，如图2所示。

图2 管道内流体速度分布

当雷诺数低于2300时，流体受黏性力影响较大，流体以分层的方式移动；当雷诺数高于2300后流体变成湍流状态，随着雷诺数的提高管道截面处各点速度分布更加均匀，此时流体的惯性力成为主导。雷诺数的计算公式如下：

式中，d ——— 管道直径

u ——— 流体流速

ρ ——— 流体密度

μ ——— 流体黏度

3仿真设置及实验方法

3.1管道模型与网格划分

建立如图 3 所示的组合双弯管和变径管 2 种管道模型示意图，分析涡流及流速突变等情况对于超声波流量计测量精度的影响。

图3 管道模型示意图

管道装置包含缓冲管道、上游阻流件、双声道超声波流量计、出口管道 4 部分，管道直径 D =40 mm。设置上游缓冲管道及出口管道长度为 10D 即可满足大多实际工况下的测量要求，此时可以调整缓冲管道长度来研究超声波流量计的最佳安装位置。利用 GAMBIT 软件建立三维管道模型，网格类型以四面体为主，采用 TGrid 方式进行划分，整体网格尺寸设为 4，对弯管处、管道变径处单独进行局部网格加密处理，局部网格尺寸设置为 2，生成网格总量约为40 万。

3.2边界条件与仿真设置

管道入口处设置为速度入口（Velocity-inlet）、管道出口处设置为自由流出口（Outflow）、其余设置为壁面条件（Wall）。管道内流动介质为甲烷，密度 0． 78 g/L，流体与壁面接触无滑移。当管道内雷诺数低于 2300时选择 Lamina 模型，当管道内气体处于湍流状态时选择 ＲNG k-ε 湍流模型进行求解；流体流动采用一阶隐式求解方法，压力-速度耦合方式采用 SIMPLE 算法。选择连续相方程、动量方程来计算流体的运动行为。连续性方程：

动量方程：

式中，ρ ——— 流体密度

t ——— 时间

u ——— 速度矢量

τ ——— 牛顿黏性应力

f ——— 流体所受体积力

为全面研究超声波流量计在各种流体流动形态下的测量精度，对操作变量参数设置如下：

（1）为使流体流动覆盖层流至湍流下多种状态，设置管道入口速度为 0． 2，0． 5，2，10，20 m/s，此时雷诺数分别为 492，1229，4916，2． 45 ×10 4，4． 91 ×10 4；（2）以 10D 位置处弯管模型、10 m/s 的管道流速为例，分析全缩探头对于管道流场速度分布的影响；（3）改变下游缓冲管道长度，设定长度在2D ～20D间，研究流量计不同安装位置下对测量结果的影响，测量点设置在距超声波流量计入口 4D 处；（4）规定5 种声道位置，其位置描述方式为声道路径到管道截面中心的距离与管道直径的比值（L/D），如表1 所示。

表1 声道位置

此外，为确保仿真精度，需要进行网格敏感性验证，对比网格总数约为 40 万和 60 万的模型在不同入口流速下其计算结果的差异，发现模拟结果对于网格密度变化的敏感性较小，由于篇幅限制分析过程在此不再赘述。

3.3实验装置与实验方法

实验室综合测试平台如图 4 所示，可以改变管径尺寸、阻流件结构、流量计类型等进行实验研究。选取部分管段及仪表作为本次实验的检测装置，进气装置提供流量稳定的天然气并将其输送进入管道系统，并通过阀门对进气流量进行调节；检测管段中安装双弯管或变径管作为上游阻流装置，在缓冲管道固定位置处安装双声道超声波气体流量计，通过测量仪表来检测实际气体流量。

实验中，流体流速从 0 ～ 20 m/s 依次递增进行测量，每次测量采集数据 80 组，通过信号处理来计算流量，与标准表进行对比。

4结语

通过 Fluent 仿真的方法对天然气管道运输中造成测量误差的影响因素进行了研究，并结合实验数据验证了仿真方法的可信性。在分析了超声波流量计探头结构对于流量计测量位置处流场分布的影响以及不同下游缓冲管道长度下流量计的测量稳定性后，对双声道超声波流量计的最优声道位置进行了讨论。结果表明，流量计全缩结构会使流体产生回流并产生负向速度；超声波流量计据上游管道距离至少为10D 才能保证相对误差变化平缓、管道内流体充分发展；通过对修正系数 K 随雷诺数的变化规律得出最优声道位置为距管道截面中心 0． 25D 处，此时修正系数随管道形状、雷诺数的变化幅度最小。研究方法及影响因素的变化趋势对于不同物性的气体测量精度的提高同样适用。