Moog 滤波器的小信号开环传递函数

我们正在分析 Moog 阶梯滤波器的行为。在本节中，我们将分析拓扑的并将滤波器的小信号开环传递函数表示为一个整体。

压控滤波器 (VCF) 是模拟合成器的支柱。但是有一个滤波器高于其他滤波器，因为它具有创造性、有效性，并且（我有充分的权威）听上去“出色”：  Moog 阶梯滤波器。

在本系列中，我们将从小信号开环分析开始分析 Moog 梯形滤波器的行为。

在上一篇文章中，我们回顾了过滤器的主要元素并分析了驱动程序部分。现在，我们将分析拓扑的（滤波器部分）并将滤波器的小信号开环传递函数表示为一个整体。

在第 1 部分中，我们看到了 Moog 梯形滤波器的完整原理图并将其简化为图 1 中所示的形式。 

 

图 1. Moog 过滤器

 

我们将拓扑分为三个元素：

驱动级中间过滤阶段输出滤波级

 这三个阶段如图 2 所示。

 

图 2. 梯形滤波器拓扑的三个元素。(a) 驱动差分对。(b) 中间阶梯低通滤波器部分。(c) 顶层的输出滤波器部分。

 

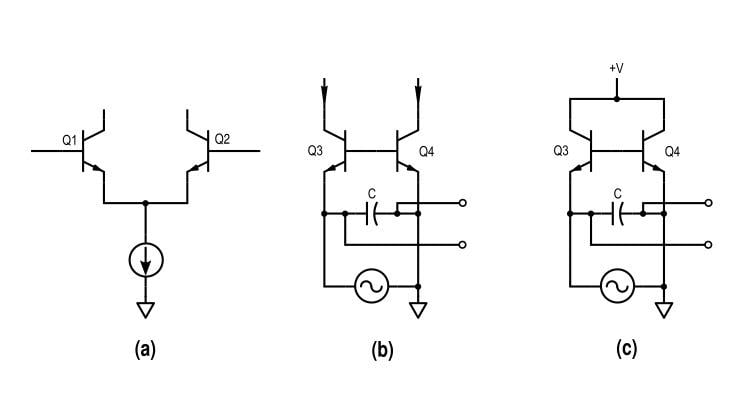
同样在第 1 部分中，我们推导出了驱动级中电压和电流之间的关系，如上图 2(a) 所示。现在，我们将分析图 2(b) 和 2(c) 中描绘的滤波器级。

Moog 滤波器的各个滤波器

滤波器部分彼此相似，不同之处在于一个驱动阶梯中的另，而另一个连接到电源。两者都采用相同的机制，因此我们将仅分析图 3 中所示的机制。

 

图 3.  Moog 滤波器中的一个滤波器部分，具有差分驱动电流。

 

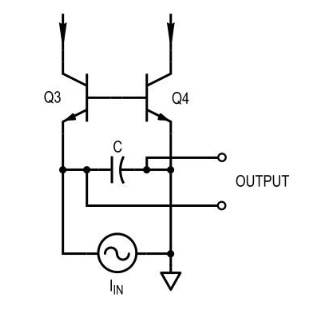
对于小信号分析，我们可以进行以下简化，如图 4、5、6 和 7 所示。

 

图 4. 利用碱基保持恒定电位这一事实，将电容器作为电抗。

 

图 5. 移除短路的晶体管。

 

图 6. 晶体管 Q3 以二极管配置连接，因此我们可以用二极管示意性地替换它。

 

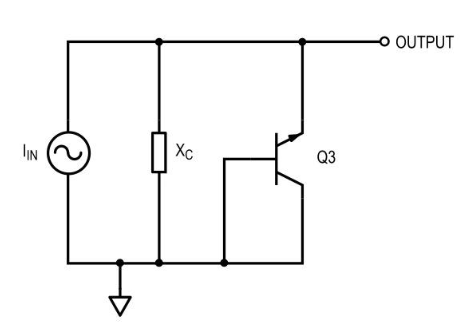
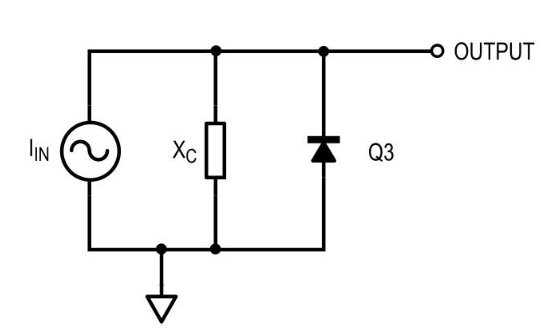
乍一看，图 7 中的电路可能不像滤波器。 

 

图 7. 二极管/晶体管终被混合 pi 模型取代。

 

这是公平的——像这样的电流驱动 RC 电路并不常见。但是，注意到两个并联组件充当分流器而不是分压器，它开始变得有意义了。

随着容抗 Xc减小（随着频率增加），电容器两端的电压减小。

该电路的输出电压是电容器两端的电压，并将传递函数描述为跨阻抗 r tr，我们发现：

 

r t r = v o u t i n _= ? 1 2 j ω C + g mrtr=voutiin=?12jωC+gm

 

在哪里

 

$${}_m=\frac{{}_C}{{}_T}$$

 

对于晶体管偏置（驱动）电流 I C，我们假设高贝塔值。

对于中间滤波器级，输出电流 g m v out成为下一部分的输入电流。这个电流是：

 

$${}_{out}={}_{in}\frac{?{}_m}{2j\omega C+{}_m}$$

 

这是我们计算开环增益所需的其他结果。

总结这个滤波器部分：我们已经证明输入电流导致电容器两端的电压降与电容电抗成正比。随着频率的增加，电压降低，给我们低通动作。它就像电容器和晶体管等效基极阻抗（跨导）之间的电流驱动 RC 滤波器。对于中间级，晶体管电流用作下一部分的输入电流，而电容器电压本身用作顶层的输出。

综合考虑：计算开环增益

我们已经描述了驱动器和过滤器部分的传递函数。现在我们准备计算开环增益。对于n个滤波器级，我们可以结合我们之前的结果（一个驱动器，n-1个中间梯形滤波器部分和一个输出滤波器部分），并找到，将输出电容器的左侧作为正：

 

$${}_{out}=\left({}_m{}_{in}\right){}^{}\left(\frac{?1}{2j\omega C+{}_m}\right)$$

 

这简化为：

 

$${}_{out}=\pm {}_{in}{}^{}$$

 

其中 $$v_{out}$$ 对n 个偶数为正，对n 个奇数为负。开环电压增益为：$${}_{üt\_}$$

 

$$A=\pm {}^{}$$

 

利用 $$g_{m}$$ 约等于 $$\frac{1}{{r_e} '}$$ 的事实，我们可以重写这是一个更熟悉的形式，$${}_{\_}$$$$\frac{1}{{}^{}}$$

 

$$A=\pm {}^{}$$

 

您可能会注意到，它与 RC 低通滤波器的传递函数非常相似，

 

$$A=\frac{1}{j\omega RC?1}$$

 

我们将在下一篇文章中详细讨论这一点。

 

图 8. Moog 阶梯滤波器行为总结。点击放大。

 

我们可以将 Moog 滤波器的行为总结如下（见图 8）：偏置电流设置晶体管的静态点，并且该电流在阶梯的两侧共享。

忽略反馈，左侧的输入电压驱动小信号电流通过分支。分支之间的差分信号会在电容器上产生电位差，从而允许进行“过滤”。一种看待这个问题的方法是，晶体管的跨阻抗与电容器一起创建了一个 RC 滤波器。

输出作为顶部电容器的电势，取决于流过该电容器的小信号电流。

至此，我们假设了一些重要的事情：

所有晶体管共享相同的 beta（即它们都匹配）。通过每个晶体管基极的电流可以忽略不计。晶体管充当理想的相关电流源（无早期效应）。所有晶体管都偏置在有源区。驱动级共模电压可以忽略不计。偏置电流源是理想的。

即使采用这些理想化，电路也会受到温度依赖性的影响（隐藏在 g m项和晶体管贝塔中）。然而，回想一下这个电路曾用于模拟合成器，这些缺陷被认为赋予了滤波器“特性”。 

 

结论

在我们分析的第二部分中，我们研究了的 Moog 梯形滤波器的小信号行为。我们做出了一些重要的假设和理想化以简化分析并得出了 n 级滤波器的通用传递函数。

展望未来，我们将通过考虑反馈来扩展我们的分析，并更详细地分析滤波器部分以了解滤波器参数。Moog 阶梯滤波器也激发了一些模仿设计的灵感，我们也将看看这些。

据我所知，这是个面向普通读者发布的 Moog 滤波器分析，我很高兴能成为向设计师介绍这种创造性和智能设计的人。