DSP 技巧：频率解调算法

一种常用的测量复杂正弦信号瞬时频率的技术是计算信号瞬时 θ( n ) 相位的导数，如下面的图 13–60所示。

图 13–60  使用反正切函数的频率解调器。

这是传统的离散信号调频解调方法，效果很好。解调器的瞬时输出频率为下面的 Eq13-111：

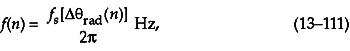
其中f s 是以赫兹为单位的采样率。

计算瞬时相位 θ( n ) 需要反正切运算，如果没有大量的计算资源，很难准确实现。这是用于计算等式Δθ( n )的方案。(13–111) 没有中间 θ( n ) 相位计算（及其讨厌的反正切函数）。我们推导出 ?θ( n ) 计算算法如下，初使用基于以下定义的连续时间变量：

i ( t ) = 同相信号，
q ( t ) = 正交相位信号，
θ( t ) = tan –1 [ q ( t )/ i ( t )] = 瞬时相位，
Δθ( t ) = 时间导数的 θ ( t )。(13-112)  

首先，我们让r ( t )= q ( t )/ i ( t ) 成为我们试图计算其反正切导数的信号。微积分恒等式tan –1 [ r ( t )]的时间导数是

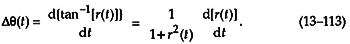
因为 d[ r ( t )]/dt = d[ q ( t )/ i ( t )]/dt，我们使用微积分恒等式对比率的导数来写

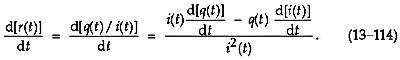
堵塞方程 (13–114) 的结果进入 Eq. (13–113)，我们有

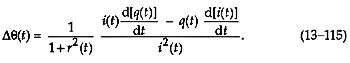
替换等式中的r ( t )。(13–115) 和q ( t )/ i ( t ) 产量

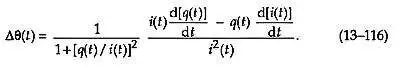
我们到了那里。接下来我们将方程式中个比率的分子和分母相乘。(13–116) 乘以i 2 ( t )，并将t替换为我们的离散时间变量索引n以得出我们的终结果

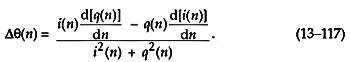
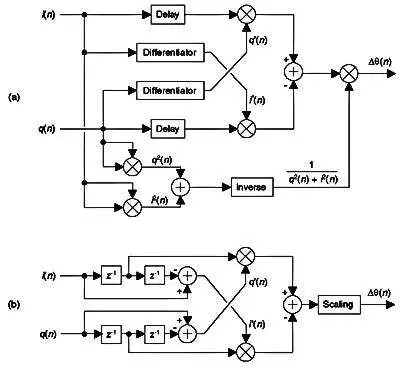
图 13–61。 无反正切频率解调器：（a）标准过程； (b) 简化程序。

图 13–61(a) 显示了该算法的实现，其中i ( n ) 和q ( n ) 的导数分别为i '( n ) 和q '( n )。Δφ( n ) 输出序列用于等式。(13–111) 计算瞬时频率。

微分器是抽头数为奇数的抽头延迟线 FIR 微分滤波器。当微分器是一个系数为 1,0,–1 的 FIR 滤波器时，参考文献 [54] 了可接受的结果。

图 13–61 中的延迟元件用于将i ( n ) 和q ( n ) 与微分器的输出进行时间对齐，以便在使用K抽头微分器时延迟为 ( K –1)/2 个样本. 实际上，可以通过关闭微分滤波器的中心抽头来获得延迟。

如果i ( n )+ jq ( n ) 信号是纯粹的 FM 和硬限制使得i 2 ( n )+ q 2 ( n ) = 常数，则方程式中的分母计算。(13–117) 不需要执行。在这种情况下，使用 1,0,–1 系数微分器，FM 解调器被简化为图 13–61(b) 中所示的解调器，其中缩放操作是乘以常数的倒数。