基于MATLAB&SIMULINK开发自动驾驶系统第四讲之线性卡尔曼滤波

卡尔曼滤波是目前行业中做感知算法和感知融合算法必用的算法，因此小明师兄和大家一起来学习一下。

当使用卡尔曼滤波器跟踪物体时，会使用一连串的探测量或测量量来构建物体运动的模型。物体运动是由物体状态的变化来定义的。卡尔曼滤波器是一种最佳的、递归的算法，用于估计物体的运动跟踪。滤波器之所以是递归的，是因为它使用之前的状态，使用可能在该区间内进行的测量来更新当前状态。卡尔曼滤波器将这些新的测量值纳入其中，以保持状态估计的尽可能准确。该滤波器是最佳的，因为它使状态的均方误差最小化。可以使用该滤波器来预测未来的状态或估计当前状态或过去的状态。

4．1 状态方程

对于自动驾驶工具箱中跟踪的大多数类型的物体，状态向量由一维、二维或三维的位置和速度组成。

从物体在x方向以恒定加速度运动的牛顿方程开始，将这些方程转换为空间状态形式：

如果定义状态作为：

可以将牛顿定律写成如下状态方程：

当对物体遵循这种类型的运动有信心时，会使用线性动态模型。有时，模型包括过程噪声，以反映运动模型的不确定性。在这种情况下，牛顿方程有一个附加项：

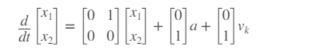
vk是加速度的未知噪声扰动。只有噪声的统计量是已知的。假设它是零均值的高斯白噪声。

可以将这种类型的方程扩展到一个以上的维度。在二维中，方程的形式为：

右侧的4×4矩阵是状态转换模型矩阵。对于独立的x和y运动，这个矩阵是块对角线。

当过渡到离散时间时，会在时间间隔的长度上整合运动方程。在离散形式中，对于T的样本区间，状态表示变成了：

量xk＋1是离散时间k＋1时的状态，xk是更早的离散时间k时的状态。如果加入噪声，方程就会变得更复杂，因为噪声的积分并不简单。

状态方程可以概括为：

Fk是状态转换矩阵，Gk是控制矩阵。控制矩阵考虑了作用在物体上的任何已知力。这两个矩阵均已给出。最后一个项代表动态模型的类似噪声的随机扰动。噪声被假定为零均值高斯白噪声。

有输入噪声的连续时间系统由线性随机微分方程描述。有输入噪声的离散时间系统用线性随机微分方程描述。状态空间表示法是一个物理系统的数学模型，其中输入、输出和状态变量由一阶耦合方程相关。

4．2 测量模型

测量是对系统的观察。测量值取决于状态矢量，但并不总是与状态矢量相同。例如，在雷达系统中，测量值可以是球面坐标，如距离、方位角和海拔，而状态矢量是笛卡尔坐标的位置和速度。对于线性卡尔曼滤波器，测量值总是状态矢量的线性函数，排除了球面坐标。要使用球面坐标，需要使用扩展卡尔曼滤波器。

测量模型假设任何时候的实际测量值都与当前状态有关，其方法是：

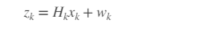
wk代表当前时间步的测量噪声。测量噪声也是零均值白高斯噪声，其协方差矩阵Q由以下方式描述：

4．3 线性卡尔曼滤波等式

如果没有噪声，则卡尔曼滤波的等式应该为：

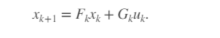
同样，测量模型也没有测量噪声贡献。在每个实例中，过程和测量噪声都是不知道的。只有噪声统计数据是已知的。噪声统计数据是已知的。

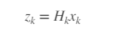
可以把这些方程放到一个递归循环中，来估计状态如何演化，也可以估计状态分量的不确定性如何演化。

4．4 滤波环

从状态的最佳估计值x0／0和状态协方差P0／0开始，滤波器在不断的循环中执行这些步骤。

1 使用运动方程将状态传播到下一步

将协方差矩阵也传播出去。

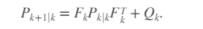
下标符号k＋1｜k表示该量是在k＋1步时从k步开始传播的最优估计，这个估计通常被称为先验估计。

然后预测更新时间的测量结果。

2 利用实际测量和预测测量的差值来修正更新时间的状态。修正需要计算卡尔曼增益。要做到这一点，首先要计算测量预测协方差（创新）。

然后卡尔曼滤波的增益为：

并由使用最优条件得出。

3 用测量值修正预测估计值。假设估计值是预测状态与测量值的线性组合。修正后的估计值使用下标符号，k＋1｜k＋1．是由以下内容计算出来的

其中Kk＋1为卡尔曼增益。修正后的状态通常被称为状态的后验估计，因为它是在包含测量之后得出的。

修正状态协方差矩阵

最后，可以根据修正后的状态来计算测量值。这不是对测量值的修正，而是对测量值的最佳估计，是基于状态的最佳估计。将其与实际测量值进行比较，就可以了解滤波器的性能。

此图总结了卡尔曼环的操作：

4．5 恒速模型

线性卡尔曼滤波器包含一个内置的线性恒速运动模型。另外，也可以指定线性运动的过渡矩阵。下一个时间步的状态更新是当前时间状态的线性函数。在这个滤波器中，测量值也是测量矩阵所描述的状态的线性函数。对于一个在三维空间中运动的物体，状态由x、y、z坐标中的位置和速度来描述。恒速运动的状态转换模型为

测量模型是状态向量的线性函数。最简单的情况是，测量值是状态的位置分量。

trackingKF 函数实例：

创建一个使用二维恒速运动模型的线性卡尔曼滤波器。假设测量由物体的X－Y位置组成。指定初始状态估计的速度为零。x ＝ 5．3；
y ＝ 3．6；
initialState ＝ ［x；0；y；0］；
KF ＝ trackingKF（＇MotionModel＇，＇2D Constant Velocity＇，＇State＇，initialState）；

从恒定速度的轨迹中创建测量的位置：

vx ＝ 0．2；
vy ＝ 0．1；
T ＝ 0．5；

pos ＝ ［0：vx＊T：2；5：vy＊T：6］＇；

预测并纠正物体的状态：

for k ＝ 1：size（pos，1）
pstates（k，：） ＝ predict（KF，T）；
cstates（k，：） ＝ correct（KF，pos（k，：））；
end

绘制跟踪曲线图：

plot（pos（：，1），pos（：，2），＇k．＇， pstates（：，1），pstates（：，3），＇＋＇， ．．．
cstates（：，1），cstates（：，3），＇o＇）
xlabel（＇x ［m］＇）
ylabel（＇y ［m］＇）
grid
xt ＝ ［x－2 pos（1，1）＋0．1 pos（end，1）＋0．1］；
yt ＝ ［y pos（1，2） pos（end，2）］；
text（xt，yt，｛＇First measurement＇，＇First position＇，＇Last position＇｝）
legend（＇Object position＇， ＇Predicted position＇， ＇Corrected position＇）

4．6 恒加速模型

线性卡尔曼滤波器包含一个内置的线性恒加速运动模型。另外，也可以指定恒加速度线性运动的过渡矩阵。线性加速度的过渡模型是

最简单的情况是，测量的是状态的位置分量。

原文标题:基于MATLAB&SIMUlink开发自动驾驶系统第四讲之线性卡尔曼滤波