随着我国加入WTO 并逐步与国际市场接轨，高性能电池的使用量正大幅度增加，作为扣式电池一种的锂锰电池正是其中之一。目前国内投产这类高能电池的厂家日益增多，市场前景十分广阔。但是大部分厂家的生产设备还停留在手工或半机械化的程度，生产效率十分低下；投资力度较大的厂家则花费数千万元购买国外进口设备，严重增加产品成本，不利于打开国际销路。现实情况迫切需要国内自主设计开发一条符合锂锰扣式电池生产工艺的自动组装生产线系统，但是应用传统设计方法很难奏效。本文旨在依据公理化设计理论进行生产系统的方案设计，利用先进的设计理念解决这一难题。
公理化设计理论将机电产品作为整体的系统来看待，通过对功能需求域及设计参数域进行的解耦与耦合分析，得出最合理的优化设计方案。
1 公理化设计理论简述
公理化设计理论（Axiomatic Design Theory）是由美国麻省理工大学的Nam P.Suh 提出的。这种理论将信息量引入设计过程，是一种可量化的设计原理。它创造性地将设计过程描述成一种映射过程，即通过选择适当的设计参数，在功能需求域（FR）和设计参数域（DP）之间建立映射，映射过程遵循独立性公理和信息公理，如图1 所示。
独立性公理即要求设计参数能保证功能需求的独立性，也就是说当调整某一个DP 来满足与之对应的FR 时，不影响其他的FR功能参数，在设计方案中每个单元都能独立地完成与之相关的所有功能域需求，单元之间只交换相关数据信息，而保持一定程度的相互独立性能，这样同时也满足信息公理的要求；信息公理即在满足功能需求的前提下，使设计方案中的信息量最小，这样能极大地简化建立数学模型的过程，同时减少设计过程中不必要因素的影响，降低控制难度和准确测量难度，方案更容易实现。
在公理化设计理论中，从功能需求域到设计参数域的映射关系被描述成向量矩阵形式，以便于量化计算。因此两者关系可表示为
{FR}=[A]{DP} （1-1）
其中{FR}为功能需求域向量表示，{DP}为设计参数域向量表示，[A]称为设计矩阵（Design Matrix）。根据独立性公理的要求，当功能需求向量个数与设计参数向量个数相等时，[A]呈现对角方阵，即
A={Aij=0 i≠j；Aij=1 i=j}
此时，[A]为非耦合矩阵，这样的设计为非耦合设计。这是满足独立性公理的最优设计方案，同时也是信息量最少的设计方案。在不能完全满足独立性公理的时候，则需要采用解耦的方法，将[A]转变为下三角矩阵，这样可以通过顺序调整各设计参数来满足功能需求，调整时不影响已满足的功能需求，其信息量在特定范围内为最小，这种设计称为解耦设计。信息量则以功能需求成功概率的倒数的对数来定义，即对于一个在基本取值全程上精度分布为均匀的功能需求来说，其信息量为
I=log（L/2ΔL） （1-2）
其中，在L 上得到L 精确值的概率
p=2ΔL/L （1-3）
在这里，L 为某一FR 的基本值，±ΔL 为其精度范围。为了应用电子计算机计算信息量，习惯于用二进制位数度量信息量，多取底数为2 的对数。这样，设计对象的总信息量即为
IT=ΣIj （1-4）
根据信息公理的要求，设计方案应尽力使IT 最小，以较小的复杂性满足功能需求。
从一个完整的机电系统来看，依据公理化设计理论，设计过程可以量化为对功能需求域和设计参数域的信息量计算。[3]通过对FR 和DP 的系统性分析，得到非耦合性设计。对于不能得到非耦合设计的，采用解耦的办法得到优化的解耦设计。同时分别计算功能需求信息量和设计参数信息量，其中设计参数又分为结构参数和时域控制参数，将计算的信息量进行比较。在保证设计域信息量满足功能域信息量的要求情况下，依据两条设计公理，寻求独立性最好的最小信息量设计方案，即最优的设计方案。
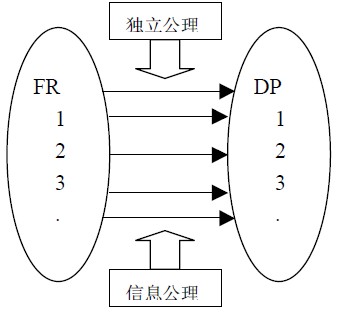
图1 原理示意图
相等时，[A]呈现对角方阵，即
A={Aij=0 i≠j；Aij=1 i=j}
此时，[A]为非耦合矩阵，这样的设计为非耦合设计。这是满足独立性公理的最优设计方案，同时也是信息量最少的设计方案。在不能完全满足独立性公理的时候，则需要采用解耦的方法，将[A]转变为下三角矩阵，这样可以通过顺序调整各设计参数来满足功能需求，调整时不影响已满足的功能需求，其信息量在特定范围内为最小，这种设计称为解耦设计。信息量则以功能需求成功概率的倒数的对数来定义，即对于一个在基本取值全程上精度分布为均匀的功能需求来说，其信息量为
I=log（L/2ΔL） （1-2）
其中，在L 上得到L 精确值的概率
p=2ΔL/L （1-3）
在这里，L 为某一FR 的基本值，±ΔL 为其精度范围。为了应用电子计算机计算信息量，习惯于用二进制位数度量信息量，多取底数为2 的对数。这样，设计对象的总信息量即为
IT=ΣIj （1-4）
根据信息公理的要求，设计方案应尽力使IT 最小，以较小的复杂性满足功能需求。
从一个完整的机电系统来看，依据公理化设计理论，设计过程可以量化为对功能需求域和设计参数域的信息量计算。[3]通过对FR 和DP 的系统性分析，得到非耦合性设计。对于不能得到非耦合设计的，采用解耦的办法得到优化的解耦设计。同时分别计算功能需求信息量和设计参数信息量，其中设计参数又分为结构参数和时域控制参数，将计算的信息量进行比较。在保证设计域信息量满足功能域信息量的要求情况下，依据两条设计公理，寻求独立性最好的最小信息量设计方案，即最优的设计方案。
